쉽고 어려운 문제, Langley의 Adventitious Angles 해결하기 이등변 삼각형 각도 문제 x
안녕하세요, 여러분. 오늘은 수학의 세계로 여러분을 초대하려고 합니다. 수학이라고 하면 어렵게 느껴지시는 분들도 계실 것 같지만, 오늘 다룰 문제는 매우 흥미로운 것이라고 자부합니다. 바로 'Langley의 Adventitious Angles'라는 문제인데요, 이 문제는 '가장 쉽고 어려운 문제'로도 불립니다. 수학을 좋아하시는 분들에게는 이미 익숙한 문제일 수 있지만, 처음 보시는 분들은 새롭게 도전해 보시는 것도 좋을 것 같습니다.
1. Langley의 Adventitious Angles란?
이 문제는 1922년에 F. B. Langley에 의해 처음 제시된 문제로, 간단히 말해 '어떤 각이 어떤 값을 가지는지'를 찾는 문제입니다. 기하학의 기본 원리를 이용해 풀 수 있지만, 조금 까다롭기도 해서 쉽고 어려운 문제라는 평가를 받았습니다.

이 문제를 풀기 위해서는 기하학의 두 가지 기본 원리를 이해해야 합니다. 첫 번째는 삼각형의 내각 합이 180도라는 원리이고, 두 번째는 이등변 삼각형에서 두 개의 동일한 각이 있다는 원리입니다. 이 두 원리를 이용하면 복잡해 보이는 문제도 한 걸음씩 근사해 갈 수 있습니다.
2. 문제 풀이 과정
그럼 본격적으로 문제를 풀어보도록 하겠습니다.
- 첫 번째로, 가상의 선을 긋는 것부터 시작합니다. ce사이에 b로부터 초록색의 가상선을 긋습니다. 이 때, 선은 bc와 길이가 같다고 가정합니다.
- 이제, ce와 만나는 점을 g라고 이름 붙여봅니다. gbc라는 각을 찾아보면, gbc는 이등변 삼각형의 등각 중 하나이므로 80도가 됩니다.
- 그다음으로, cbg라는 각은 얼마일까요? 180 - 80(각 gbc) - 80(각 gcb) = 20도가 됩니다.
- 이제, ebg라는 각은 얼마인지 계산해봅니다. 180 - 80(각 gbc) - 60(각 cbg) = 40도가 됩니다.
- 이제 삼각형 fcb를 보겠습니다. 각 bcf와 각 bfc는 각각 50도이므로, 이는 이등변 삼각형의 특성에 따라 변 bf와 변 bc가 동일합니다.
- 변 bg와 변 bc의 길이가 같으므로, 삼각형 bgf는 내각이 각각 60도인 정삼각형이 됩니다.
- 따라서, fge라는 삼각형에서 각 fge는 40도이고, 변 fg와 변 eg가 같으므로 이등변 삼각형의 원리에 따라 각 feg와 각 efg는 (180 - 40) ÷ 2 = 70도가 됩니다.
- 마지막으로, 각 feg = 70 = 40 + x이므로 x = 30도를 구할 수 있습니다.

3. 정리
이렇게 해서 Langley의 Adventitious Angles 문제를 풀 수 있습니다. 문제를 풀면서 이등변 삼각형의 등각과 등변이 같다는 것을 이용하였습니다. 이런 방식으로 문제를 풀어나가면 처음에는 복잡해 보이는 문제도 조금씩 해결해 나갈 수 있습니다.
| 단계 | 설명 |
| 1 | ce사이에 b로부터 가상의 선을 긋고, ce와 만나는 점을 g라고 명명합니다. |
| 2 | 각 gbc를 구하면, 이는 80도입니다. |
| 3 | 각 cbg를 구하면, 이는 20도입니다. |
| 4 | 각 ebg를 구하면, 이는 40도입니다. |
| 5 | 삼각형 fcb에서 각 bcf와 bfc는 각각 50도입니다. 이등변 삼각형의 원리에 따라 변 bf와 변 bc가 동일합니다. |
| 6 | 변 bg와 변 bc의 길이가 같으므로, 삼각형 bgf는 내각이 각각 60도인 정삼각형이 됩니다. |
| 7 | fge라는 삼각형에서 각 fge는 40도이고, 변 fg와 변 eg가 같으므로 이등변 삼각형의 원리에 따라 각 feg와 각 efg는 각각 70도가 됩니다. |
| 8 | 각 feg = 70 = 40 + x이므로, x는 30도를 구할 수 있습니다. |
이렇게 보니 어떤가요? 처음에는 어렵게 느껴지던 문제가 차근차근 해결되는 과정을 보며, 수학의 매력을 느끼셨기를 바랍니다.
6÷2(1+2)의 답은 9일까 1일까? 정답은 "9", 8 ÷ 2(2 + 2)는? 사칙연산 규칙
여러분이 SNS 상에서 마주칠 수 있는 가장 이슈가 되는 수학 문제 중 하나가 '6÷2(1+2)는 얼마일까?'입니다.
페이스북, 트위터, 유튜브 등 수많은 소셜 미디어에서 이 문제에 대한 토론이 벌어진 적이 있습니다.
오늘, 저는 여러분에게 이 문제의 정확한 해답을 설명해드릴 것입니다.
지금부터 제 글을 따라 오신다면 이 수학 문제의 정확한 답을 알 수 있을 것입니다.
[6÷2(1+2) 연산 순서에 따른 해석]
이 문제를 이해하는 핵심은 연산 순서, 즉 'PEMDAS/BODMAS'를 이해하는 것입니다. PEMDAS는 괄호(Parentheses), 지수(Exponents), 곱셈/나눗셈(Multiplication-Division), 덧셈/뺄셈(Addition-Subtraction) 순으로 계산하라는 원칙을 나타내며, BODMAS는 Bracket, Orders, Division-Multiplication, Addition-Subtraction 순으로 계산하라는 원칙입니다.
모든 사람들이 동의하는 첫 단계는, 괄호 안의 덧셈을 먼저 계산하는 것입니다.
6÷2(1+2) = 6÷2(3)
이 지점부터 의견이 갈리기 시작합니다.

[정답은 9]
만약 여러분이 계산기, 구글, 또는 WolframAlpha에 6÷2(3)을 입력한다면, 괄호를 암시적인 곱셈으로 변환한 후 계산을 시작할 것입니다.
6÷2(3) = 6÷2×3
사칙연산 규칙 순서에 따르면, 나눗셈과 곱셈은 같은 우선순위를 가지므로 왼쪽에서 오른쪽으로 순서대로 계산합니다. 따라서 먼저 6을 2로 나누고, 그다음 결과에 3을 곱하게 됩니다.
6÷2 ×3 = 3×3 = 9
따라서, 이 문제의 답은 '9'가 됩니다.
이것이 현재의 표기법을 기준으로 이 표현식을 평가하는 정확한 답입니다.
[100년 전의 해석: 답은 1]
하지만 이 문제에 대한 해석은 시대에 따라 다르게 해석될 수 있습니다. 만약 100년 전인 1917년에 이 문제를 봤다면 어떻게 해석했을까요?
과거에는 나눗셈 기호(÷)가 기호 오른쪽의 전체 곱셈을 나누는 것을 의미하곤 했습니다.
6÷2(3) = 6÷(2(3)) (주의: 이것은 구식 표기법입니다!)
이런 해석으로 가면, 연산 순서에 따라 괄호 안의 곱셈을 먼저 계산합니다. 2와 3을 곱한 결과를 6으로 나누게 됩니다.
6÷(2(3)) = 6÷6 = 1
이렇게 답이 '1'이 나옵니다. 하지만 이것은 구식 표기법에 따른 해석이며 현재로서는 정확한 답이 아닙니다.
[나눗셈 기호의 역사적 사용]
과거에는 나눗셈 기호가 나눗셈의 전체 대상이 나눗셈 기호 오른쪽의 표현식임을 나타내는 데 사용되었습니다. 예를 들어,
9a2÷3a = 3a (주의: 이것은 구식 표기법입니다!)
나눗셈 기호 오른쪽의 전체 곱셈이 나눗셈의 대상이 됩니다.
9a2÷3a = 9a2÷(3a) (주의: 이것은 구식 표기법입니다!)
오늘날에는 이러한 사용법이 혼란스러움을 일으키므로 거의 사용하지 않으며, 괄호를 사용하여 나누는 대상을 명확하게 표시하거나, 표현식을 설명합니다. 이제는 수학적 표현이 훨씬 쉬워져 나눗셈 기호(÷) 대신 분자와 분모가 수직으로 배열된 분수 형태를 사용합니다.
그런데 이 문제를 특정 계산기들은 여전히 1로 답을 내는 경우도 종종 있다곤 합니다.
하지만 일단 구글이든 네이버든 다음이든 포털에 저 수식을 넣기만 해도 답은 9로 나옵니다.

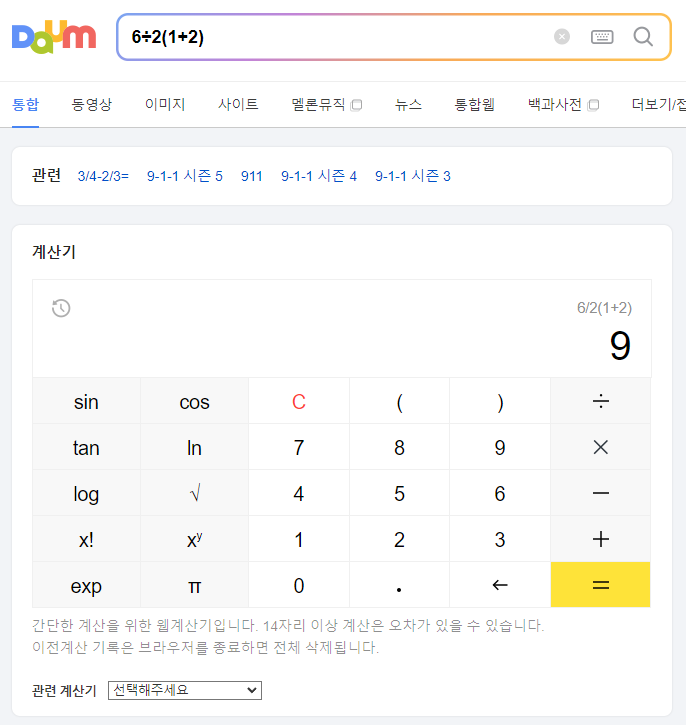
워낙 이슈가 됐었던 문제기 때문에, 딱 정한 것이죠.
수학은 계산에 주관적 관점이나 개인의 의견을 반영하지 않습니다.
정해진 규칙에 철저히 따라야죠.
[관련 문제] '8 ÷ 2(2 + 2) =?'
2019년에는 '8 ÷ 2(2 + 2) =?'라는 문제가 화제가 되었습니다.
위에서 다룬 것과 완전히 같은 문제입니다.

2019년에 화제가 됐었죠.
인터넷 커뮤니티에서는 1이 정답이라는 사람들과 16이 정답이라는 사람들 사이에서 활발한 논의가 이어지고 있습니다. 그렇다면 이 수식의 정답은 무엇일까요?
수학에는 계산 순서를 결정하는 명확한 규칙이 있습니다. 이는 수학을 배울 때 가장 먼저 익혀야 하는 사항 중 하나이며, 사칙연산 규칙을 따르지 않으면 틀린 답을 도출할 수 있습니다. 이를 통해 우리는 수학뿐만 아니라 사회에서도 규칙을 준수하는 것이 얼마나 중요한지를 배우게 됩니다.
이 수식을 이해하는 데 필요한 계산 순서에 대한 기본 규칙은 PEMDAS 혹은 BODMAS라고 불립니다. PEMDAS는 괄호(Parentheses), 지수(Exponents), 곱셈(Multiplication), 나눗셈(Division), 덧셈(Addition), 뺄셈(Subtraction)의 첫 글자를 따온 것입니다. BODMAS는 괄호(Brackets), 거듭제곱(Order), 나눗셈(Division), 곱셈(Multiplication), 덧셈(Addition), 뺄셈(Subtraction)을 나타냅니다. 이 두 규칙은 본질적으로 같은 의미를 가지고 있으며, 연산의 우선순위를 명확히 합니다.
| 연산 | PEMDAS | BODMAS |
| 1순위 | 괄호(Parentheses) | 괄호(Brackets) |
| 2순위 | 지수(Exponents) | 거듭제곱(Order) |
| 3순위 | 곱셈/나눗셈(Multiplication/Division) | 곱셈/나눗셈(Division/Multiplication) |
| 4순위 | 덧셈/뺄셈(Addition/Subtraction) | 덧셈/뺄셈(Addition/Subtraction) |
그럼 이제 원래의 수식 '8÷2(2+2)'를 풀어보겠습니다. 먼저, 괄호 안의 계산부터 해야 합니다. 그러면 2+2는 4이므로, 수식은 '8÷2x4'로 바뀝니다. 이제 곱셈과 나눗셈을 왼쪽에서 오른쪽으로 차례대로 계산합니다. 즉, 먼저 8을 2로 나눈 결과인 4를 구하고, 그다음 4를 4로 곱해서 16을 얻습니다. 따라서, 이 수식의 정답은 16입니다.
이런 혼란을 일으키는 수식은 대부분 정확한 표현을 사용하지 않아서 생기는 문제입니다. 사실, 이런 수식은 프로 수학자들 사이에서는 거의 사용되지 않습니다. 프로 수학자들은 보통 정확한 표현을 사용하여 계산 순서를 명확히 표시합니다.
결국 이 이야기를 통해 우리가 배울 수 있는 점은, 수학에는 규칙이 있고, 그 규칙을 준수하는 것이 중요하다는 것입니다. 특히나 이러한 규칙을 이해하고 따르는 것은 수학뿐만 아니라 우리의 일상생활에서도 중요한 역할을 합니다. 때때로 이런 혼란스러운 문제가 생길 수 있지만, 그럴 때마다 기본적인 규칙을 잊지 않는다면 항상 옳은 답을 찾을 수 있을 것입니다.
마지막으로, 이런 문제에 너무 많은 시간을 쏟아부을 필요는 없다고 생각합니다. 중요한 것은 학습과정에서 문제 해결을 통해 규칙을 이해하고, 그것을 우리의 삶에 적용하는 것입니다. 수학은 그 자체가 중요한 것이 아니라, 우리가 그를 통해 배우는 것이 중요합니다. 이런 시각에서 보면, 이 문제는 우리에게 규칙의 중요성을 깨닫게 해주는 좋은 기회가 되었던 것 같습니다.
여러분들도 이런 문제를 통해 어떤 규칙을 배울 수 있었나요? 아래 댓글로 여러분의 생각을 나누어 주세요. 다음에도 또 재미있는 이야기로 찾아뵙겠습니다. 그럼, 다음 글에서 만나요!
[참조 문헌]
- http://www.slate.com/articles/health\_and\_science/science/2013/03/facebook\_math\_problem\_why\_pemdas\_doesn\_t\_always\_give\_a\_clear\_answer.html
- Lennes, N. J. “Discussions: Relating to the Order of Operations in Algebra.” The American Mathematical Monthly 24.2 (1917): 93-95. Web. http://www.jstor.org/stable/2972726?seq=1#page\_scan\_tab\_contents
- [If Math Is Universal, Why Can’t It Answer a Stupid Facebook Problem?
'건강 과학 생물 천문 식품' 카테고리의 다른 글
| 29일 부분월식 시간. 2025년 9월 개기 월식 원리 (0) | 2023.10.22 |
|---|---|
| 다이슨 날개 없는 선풍기 원리 단점 (0) | 2023.10.10 |
| 명아주 나물 효능 지팡이 청려장 (0) | 2023.07.10 |
| 이름으로 오해받는 동물들: 전기뱀장어, 산양, 갈기늑대, 킹코브라, 공작사마귀새우, 뿔도마뱀, 하루살이, 동방임금딱새 (0) | 2023.06.20 |
| 걸어 다니는 벌금 쿼카 캐릭터 인형 (0) | 2023.06.18 |



