에라토스테네스의 체 자바스크립트 소수 찾기 알고리즘 만들기
자바스크립트를 이용하여 소수를 찾는 로직을 구현하는 것은 프로그래밍 실력을 향상시키는 훌륭한 방법입니다. 소수 찾기 알고리즘은 기본적인 수학적 개념과 컴퓨터 과학의 기본을 결합한 예제로, 프로그래밍 능력을 향상시킬 뿐만 아니라 알고리즘에 대한 이해도를 높이는 데에도 도움이 됩니다. 이 글에서는 자바스크립트를 사용하여 소수를 찾는 여러 가지 방법과 그들의 효율성에 대해 알아보겠습니다.
소수에 대한 기본 개념 이해
먼저 소수란 무엇인지 이해해야 합니다. 소수는 1과 자기 자신만을 약수로 가지는 1보다 큰 자연수를 말합니다. 예를 들어, 2, 3, 5, 7, 11 등은 소수입니다. 중요한 점은 1은 소수가 아니라는 것입니다. 소수 판별 로직을 구현하기 전에 이 기본적인 개념을 명확히 해야 합니다.

소수 판별 기본 알고리즘
소수를 판별하는 가장 기본적인 방법은 2부터 (n-1)까지의 모든 수로 n을 나누어 보는 것입니다. 만약 n이 어떤 수로도 나누어지지 않으면, 그 수는 소수입니다.
function isPrime(n) {
if (n <= 1) return false; // 1은 소수가 아니다
for (let i = 2; i < n; i++) {
if (n % i === 0) return false;
}
return true;
}이 방법은 이해하기 쉽고 구현하기 간단하지만, n이 커질수록 비효율적입니다.
효율적인 소수 판별 방법
보다 효율적인 방법은 n의 제곱근까지만 확인하는 것입니다. n의 제곱근 이상의 약수는 n의 제곱근 이하의 약수와 쌍을 이루기 때문에, 제곱근까지만 확인해도 충분합니다.
function isPrime(n) {
if (n <= 1) return false; // 1은 소수가 아니다
for (let i = 2; i * i <= n; i++) {
if (n % i === 0) return false;
}
return true;
}이 방법은 이전 방법보다 훨씬 빠르며, 큰 수에 대해서도 효율적으로 소수를 판별할 수 있습니다.
에라토스테네스의 체 자바스크립트 소수 찾기 알고리즘
다수의 소수를 찾을 때 효율적인 방법 중 하나는 '에라토스테네스의 체'를 사용하는 것입니다. 이 방법은 특정 범위 안의 모든 소수를 찾을 때 사용됩니다. 기본적으로는 2부터 시작하여 그 수의 배수를 모두 제거하는 방식으로 진행됩니다.
function findPrimes(limit) {
let primes = [];
let sieve = new Array(limit + 1).fill(true);
sieve[0] = sieve[1] = false; // 0과 1은 소수가 아님
for (let i = 2; i <= limit; i++) {
if (sieve
[i]) {
primes.push(i);
for (let j = i * 2; j <= limit; j += i) {
sieve[j] = false;
}
}
}
return primes;
}이 방법은 범위 내에서 반복적으로 소수를 찾아야 할 때 매우 유용합니다.
자바스크립트로 소수를 찾는 로직을 구현하는 것은 다양한 프로그래밍 기술을 익히는 데 도움이 됩니다. 이러한 기본적인 알고리즘을 이해하고 구현하는 것은 프로그래밍 능력을 키우는 데 중요한 단계입니다. 또한, 이러한 알고리즘은 웹 개발, 데이터 분석, 암호학 등 다양한 분야에서 응용될 수 있습니다.
에라토스테네스의 체의 원리와 역사
에라토스테네스의 체는 수학과 컴퓨터 과학 분야에서 소수를 찾는 가장 효율적인 방법 중 하나로 널리 알려져 있습니다. 이 방법은 고대 그리스 수학자 에라토스테네스에 의해 개발되었으며, 그의 이름을 따서 명명되었습니다. 이 방법의 핵심은 특정 범위 내의 모든 소수를 신속하고 정확하게 찾아내는 것입니다.


에라토스테네스의 체의 작동 원리
에라토스테네스의 체는 다음과 같은 단계로 소수를 찾습니다:
- 초기화: 처음에는 모든 숫자가 소수일 가능성이 있다고 가정하고 시작합니다.
- 필터링: 가장 작은 소수인 2부터 시작하여, 해당 소수의 배수를 모두 제거합니다. 예를 들어, 2의 배수인 4, 6, 8 등을 리스트에서 제거합니다.
- 반복: 다음으로 작은 소수를 찾고, 그 배수를 다시 제거합니다. 이 과정은 리스트에 더 이상 배수를 제거할 수 없을 때까지 반복됩니다.
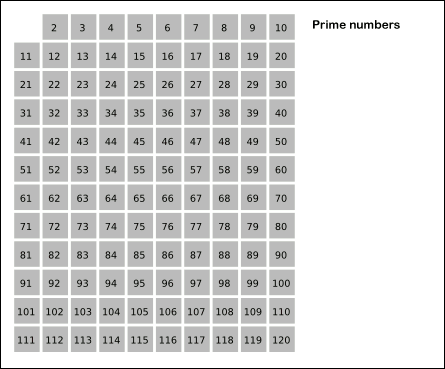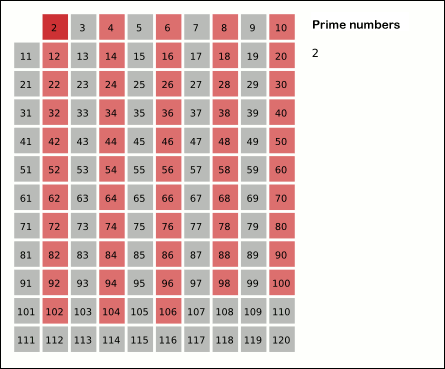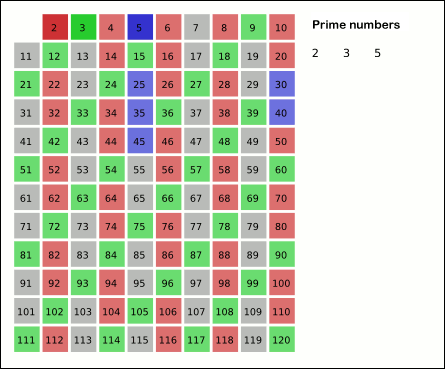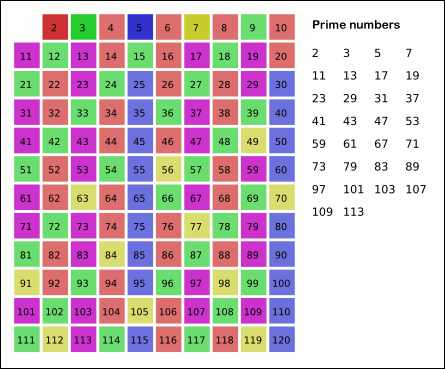
- 결과: 마지막으로 남은 숫자들이 바로 해당 범위 내의 모든 소수입니다.
지구 둘레를 측정했던 에라토스테네스
에라토스테네스는 기원전 276년 경에 태어나 기원전 194년경 사망한 고대 그리스의 수학자, 천문학자, 지리학자였습니다. 그는 특히 지구의 둘레를 측정하는 데 있어서 중요한 업적을 남겼으며, ‘에라토스테네스의 체’는 그의 이름을 딴 또 다른 중요한 발명품입니다. 이 방법은 소수를 찾는 가장 초기의 알려진 방법 중 하나이며, 수학과 컴퓨터 과학에서 오늘날까지도 중요한 위치를 차지하고 있습니다.


에라토스테네스의 체의 현대적 적용
에라토스테네스의 체는 현대에도 다양한 분야에서 활용됩니다. 특히 컴퓨터 과학에서 알고리즘의 기초적인 구성 요소로 자주 사용됩니다. 암호학, 네트워크 보안, 데이터 분석 등의 분야에서 소수의 중요성은 매우 크며, 이러한 분야에서 소수를 효율적으로 찾기 위한 방법으로 에라토스테네스의 체가 자주 채택됩니다.
컴퓨터 과학에서의 응용
컴퓨터 과학에서는 소수를 사용하여 데이터를 암호화하고 해독하는 데 필수적인 역할을 합니다. 이 때문에 소수를 신속하고 정확하게 찾는 것이 매우 중요한데, 에라토스테네스의 체는 이러한 목적에 아주 적합한 알고리즘입니다. 또한, 프로그래밍에서도 소수를 찾는 연습 문제로 자주 등장하며, 알고리즘을 이해하고 구현하는 능력을 키우는 데 도움을 줍니다.
에라토스테네스의 체는 수학과 컴퓨터 과학에서 여전히 중요한 위치를 차지하는 고대의 발명품입니다. 이 알고리즘은 단순하지만 매우 효과적이며, 현대의 다양한 기술적 문제를 해결하는 데 기여하고 있습니다. 에라토스테네스의 지적 유산은 시간이 지나도 그 가치를 잃지 않으며, 앞으로도 계속해서 중요한 역할을 할 것으로 보입니다.
'IT 모바일 Gear Up' 카테고리의 다른 글
| PDF 용량 줄이기 무료 사이트 사용 방법 (0) | 2023.11.21 |
|---|---|
| React Query 리액트 쿼리 v5 에서 바뀐 점 (0) | 2023.11.20 |
| 엑셀 시간 더하는 방법 Excel 시간 더하기 24시간 초과 빼기 (0) | 2023.11.18 |
| 구글 크롬 번역기로 바로 웹 페이지 번역하는 여러가지 방법 (0) | 2023.11.17 |
| 파워포인트 엑셀 차트 복사 PPT 표 추가하는 방법 연결하여 붙여넣기 데이터 링크: 엑셀과 파워포인트 자료 연동 (0) | 2023.11.14 |



