이등변 삼각형 빗변의 길이 구하는 공식
이등변 삼각형은 두 변의 길이가 같은 특징을 가진 삼각형으로, 기하학에서 자주 등장하는 도형입니다. 이러한 삼각형에서 빗변은 주어진 변들의 길이와 각도에 따라 정확히 계산할 수 있습니다. 특히, 이등변 삼각형의 빗변을 구하는 공식은 수학적 사고를 필요로 하며, 다양한 응용 문제에서 활용됩니다. 이번 포스팅에서는 이등변 삼각형의 빗변 길이를 구하는 공식을 상세히 설명하고, 이를 실제 문제에 어떻게 적용할 수 있는지 알아보겠습니다. 더불어 관련 개념과 공식의 응용에 대해서도 심도 있게 살펴보겠습니다.
이등변 삼각형의 기본 정의와 특징
이등변 삼각형은 두 변의 길이가 같고, 이 두 변 사이에 포함된 각이 중요한 역할을 합니다. 이등변 삼각형은 다음과 같은 특징을 가집니다:
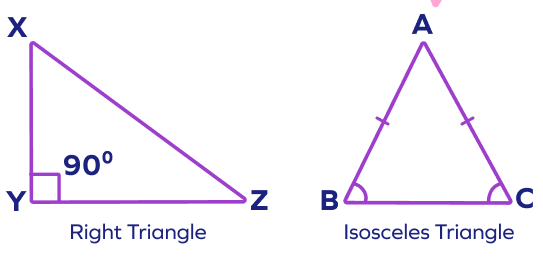
- 두 변의 길이가 동일하다.
- 두 동일한 변의 반대쪽 각이 동일하다.
- 꼭짓점에서 밑변까지의 수직선(높이)이 밑변을 정확히 반으로 나눈다.
- 이등분된 밑변의 길이는 대칭적 구조를 강조하며, 높이와 삼각형의 비례 관계를 결정짓는다.
이러한 특성은 빗변 길이를 구하는 공식을 도출하는 데 중요한 기초가 됩니다. 이등변 삼각형은 기하학적 계산뿐만 아니라 실생활에서도 구조적 안정성과 균형을 나타내는 도형으로 자주 활용됩니다.
빗변의 길이 구하는 공식
이등변 삼각형의 빗변을 구하기 위해 삼각함수를 활용할 수 있습니다. 아래는 대표적인 방법입니다:
1. 삼각함수를 이용한 공식
이등변 삼각형에서 두 변의 길이를 $a$라고 하고, 포함각을 $\theta$라고 할 때, 빗변의 길이 $c$는 다음과 같이 구할 수 있습니다:
$$
c = \sqrt{2a^2 (1 - \cos(\theta))}
$$
이 공식은 코사인 법칙에서 유도된 것으로, 삼각형의 대칭성을 활용합니다. 포함각 $\theta$는 두 동일한 변 사이의 각도를 의미합니다. 이 공식은 비대칭 삼각형의 경우에도 확장하여 사용할 수 있는 기초 공식을 제공합니다.
2. 피타고라스 정리를 이용한 공식 (특수한 경우)
만약 이등변 삼각형이 직각 이등변 삼각형일 경우, 빗변의 길이는 피타고라스 정리를 이용하여 간단히 계산할 수 있습니다. 이때 빗변 $c$는 다음과 같습니다:
$$
c = a\sqrt{2}
$$
이는 직각삼각형의 특수한 경우로, 포함각이 $90^\circ$일 때 적용됩니다. 이와 같은 경우는 많은 기하학적 구조에서 빈번히 등장하며, 특히 건축이나 설계에서 안정적 구조를 분석하는 데 사용됩니다.
3. 포함각이 120도 이상인 경우
포함각이 $120^\circ$ 이상인 경우, 삼각형의 형태가 더욱 길쭉해지며, 빗변의 계산이 중요한 역할을 합니다. 이러한 경우에도 코사인 법칙을 사용하여 쉽게 계산할 수 있습니다. $\cos(\theta)$ 값이 음수가 되는 점을 고려하여 다음과 같은 공식을 사용할 수 있습니다:
$$
c = \sqrt{2a^2 (1 - \cos(\theta))}
$$
이 공식은 삼각형의 모든 유형에 보편적으로 적용 가능합니다.
실제 사례를 통한 공식 적용
예제 1: 포함각이 60도인 이등변 삼각형
두 변의 길이가 각각 5인 이등변 삼각형이 있습니다. 이때 포함각 $\theta$가 60도라면 빗변의 길이는 다음과 같이 계산됩니다:
$$
c = \sqrt{2(5)^2(1 - \cos(60^\circ))}
$$
$$
= \sqrt{2(25)(1 - 0.5)} = \sqrt{25} = 5
$$
이 경우, 빗변의 길이는 원래 주어진 변의 길이와 동일하게 유지됩니다. 이는 포함각에 따라 빗변이 변화하는 특성을 잘 보여줍니다.
예제 2: 직각 이등변 삼각형
길이가 7인 두 변을 가진 직각 이등변 삼각형에서 빗변은 다음과 같이 계산됩니다:
$$
c = 7\sqrt{2} \approx 9.899
$$
직각 이등변 삼각형은 실생활에서 매우 흔히 등장하는 형태로, 특히 사다리 구조, 경사면의 계산 등 다양한 상황에서 활용됩니다.
예제 3: 포함각이 120도인 경우
두 변의 길이가 10이고 포함각이 $120^\circ$인 이등변 삼각형에서 빗변은 다음과 같이 계산됩니다:
$$
c = \sqrt{2(10)^2 (1 - \cos(120^\circ))}
$$
$$
= \sqrt{2(100)(1 - (-0.5))} = \sqrt{2(100)(1.5)} = \sqrt{300} \approx 17.32
$$
이 예시는 빗변이 포함각의 크기에 따라 크게 달라질 수 있음을 보여줍니다.
결론
이등변 삼각형의 빗변을 구하는 공식은 삼각형의 대칭성과 삼각함수를 이용한 수학적 접근으로 간단히 도출할 수 있습니다. 이러한 공식을 활용하면 기하학 문제뿐만 아니라 다양한 실생활 문제를 해결하는 데에도 큰 도움이 됩니다. 특히 삼각형의 특성과 포함각의 조건을 정확히 이해하면, 문제 해결 과정이 훨씬 더 명확해집니다. 이 글에서 다룬 다양한 사례와 응용 방식을 바탕으로, 이등변 삼각형의 빗변 길이 계산을 더욱 자신 있게 적용할 수 있기를 바랍니다.
'건강 과학 생물 천문 식품' 카테고리의 다른 글
| 삭센다 부작용, 가격 - 실제 사용 경험 후기 (0) | 2025.01.26 |
|---|---|
| 스타틴 부작용, 비 스타틴 계열 고지혈증 약 종류 (0) | 2025.01.24 |
| 평행사변형 넓이 구하는 공식 유도 (0) | 2025.01.20 |
| 섭씨 화씨 변환표 계산, 유래 (0) | 2025.01.17 |
| 스페이스x 우주선 스타십 공중폭발 영상 별빛이 내린다 샤랄라~ (0) | 2025.01.17 |



